El-Haj Laamri est maître de conférences à l'Université de Lorraine. Mathématicien de formation, il effectue ses recherches à l’Institut Elie Cartan de Lorraine, ses thématiques de recherche portent sur les Équations aux Dérivées Partielles et leurs applications.
Jean Mawhin, professeur émérite en mathématiques à l’Université Catholique de Louvain et membre de l’Académie Royale de Belgique a échangé sur le nombre d’or avec El Haj Laamri, enseignant-chercheur en mathématiques à l’occasion de sa conférence du 31 janvier dans le cadre du cycle de conférences Sciences et Société de l’université de Lorraine.
El Haj Laamri : On célèbre cette année les 500 ans de Léonard de Vinci, célèbre pour avoir inscrit le nombre d’or dans la prospérité, notamment à travers son utilisation dans ses peintures et planches. Mais d’où vient cet étrange nombre « parfait » ?
Jean Mawhin : Son histoire est une véritable saga qui court sur plusieurs millénaires. Les premières traces écrites du nombre d’or se trouvent dans les célèbres « Éléments » d’Euclide, au 3e siècle avant JC, qui proposent un état structuré des mathématiques de l’époque. Trois siècles auparavant, les pythagoriciens avaient cherché (on ne dispose pas d’écrits, cette secte ayant le goût du secret), à expliquer le cosmos par des nombres entiers ou des quotients de tels nombres. Ils avaient découvert qu’il était impossible d’exprimer de la sorte le rapport de la longueur de la diagonale d’un carré avec celle de son côté. Auraient-ils plus de chance avec le pentagone, la version étoilée étant leur signe de ralliement ?
Cet intérêt pour les polygones réguliers (côtés égaux) conduisit au problème de leur inscription dans un cercle en utilisant seulement la règle et le compas. Si la construction est facile pour le triangle, le carré ou l’hexagone, elle s’avère plus difficile pour le pentagone ou le décagone. Sa solution requiert la possibilité, dans les mêmes conditions, de découper un segment de droite en deux morceaux inégaux de sorte que la longueur du segment divisée par celle du grand morceau soit égale à la longueur du grand morceau divisée par celle du petit morceau. Cette valeur commune des deux rapports est le futur nombre d’or.
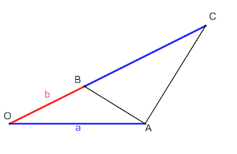
Euclide l’appelle la « division en moyenne et extrême raison » ou la « section ». Il montre comment résoudre le problème et applique le résultat pour inscrire dans une sphère deux des cinq polyèdres réguliers (les « solides platonicien »)), le dodécaèdre (douze faces pentagonales égales) et l’icosaèdre (vingt faces triangulaires égales).
Ce n’est qu’aux XVIIe et XVIIIe siècles que des mathématiciens, avec le développement de la notation décimale et de l’algèbre, vont donner la valeur numérique du rapport de la division en moyenne et extrême raison : 1,618… = (1+√5)/2. Ce n’est qu’au XXe siècle qu’on le baptise Phi (Φ) en l’honneur de Phydias, l’architecte du Parthénon.
Comment le nombre d’or s’exprime-t-il dans la peinture et l’architecture ?
Au Moyen-âge, des cathédrales gothiques comme celles d’Amiens et d’Auxerre attestent de la présence du pentagone et du décagone. Il semble que ces figures fascinent les compagnons tailleurs de pierre et maçons qui souhaitent ainsi montrer leur savoir et savoir-faire tout en gardant secret les procédés de fabrication de leurs œuvres.
À la renaissance italienne, un moine voyageur et exalté, Luca Pacioli, réunit, dans un style enthousiaste, tout ce qu’Euclide contient sur la section, en un livre intitulé « La divine proportion ». Son ami Léonard de Vinci en réalise les illustrations. Le style particulier et ronflant de l’écrit remet le concept du nombre d’or au goût du jour. Son auteur, en proposant même un lien avec Dieu et la Sainte Trinité, fait un pas vers une interprétation ésotérique avec sa « théologie géométrique ».

Au XIXe siècle, l’Allemagne voit l’essor d’une esthétique scientifique qui cherche à caractériser la beauté par un minimum de nombres. Sous l’impulsion d’Adolph Zeising, la section d’or, nouvel intitulé de la divine proportion, devient la norme esthétique. Le philosophe allemand produit un manifeste assez radical qui prétend que la section d’or est omniprésente – dans le corps humain, la structure des animaux, l’architecture, la peinture, la sculpture – et que sa présence rend les choses plus belles. En quelque sorte, il encapsule la beauté dans un seul nombre. Ses affirmations et ses mesures (notamment celles de la pyramide de Khéops et du Parthénon, en ruine) sont toutefois considérées comme approximatives et sujettes à caution.
Certains artistes utiliseront par la suite le nombre d’or de façon affirmée et assumée. L’architecte Le Corbusier a ainsi défini un système de mesure (concept architectural avec les rapports en lien avec le nombre d’or) appelé le Modulor. Le peintre Salvador Dali l’a volontairement introduit dans certaines de ses œuvres, comme sa Leda Atomique ou sa Demi-tasse géante volante. D’autres peintres auraient aussi cédé aux charmes du nombre d’or, sans que l’on sache véritablement si leurs utilisations étaient volontaires, fortuites, inconscientes ou intentionnelles, ou s’il s’agit de fractions proches de Phi. C’est le cas notamment de Botticelli et de… Léonard de Vinci !
Le nombre d’or a aussi un côté sombre…
Certaines références au nombre d’or relèvent de dérives regrettables, erreurs et propos douteux. Par exemple, un ingénieur tourné astrologue, Maurice Rougie, a publié en 1946 sous le pseudonyme de Dom Neroman, « Le nombre d’or à la portée de tous ». Cet ouvrage, non seulement propose des relations entre Phi et d’autres nombres célèbres aussi séduisantes que fausses, et contient des affirmations dépourvues de sens comme « le nombre d’or est à la fois irrationnel et entier ». Bien pire, en partant d’un canon de la beauté humaine imposant un rapport entre taille et hauteur du nombril égal à Phi, Dom Neroman a avancé certaines conclusions racistes.
La beauté ne peut pas se réduire à un seul nombre : c’est réductionniste, triste et dangereux. Le nombre d’or est un concept intéressant qui a joué et joue encore un grand rôle dans divers domaines mathématiques, mais il faut rester vigilant face à certaines conséquences que certains en tirent, à sa prétendue universalité et aux considérations occultes dont il peut faire l’objet.
![]()
El Haj Laamri, enseignant-chercheur en mathématiques, Université de Lorraine
Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.

