Temps de lecture : 4 minutes
Étienne Corman, chargé de recherche CNRS au sein de l’équipe Pixel du Loria, (CNRS – Université de Lorraine), vient d’être lauréat d’un Best Paper Award – Honorable Mention lors de Siggraph 2025 ! Ce prix récompense son article « Rectangular Surface Parameterization » co-écrit avec Keenan Crane, professeur à Carnegie Mellon University.
Siggraph est la conférence internationale phare pour l’infographie et les techniques interactives. Cette année, l’événement a eu lieu à Vancouver (Canada) du 10 au 14 août.
Cet article sur la génération de maillages pour la simulation numérique a été sélectionné parmi plus de 970 soumissions a été présenté lors du programme « Technical Papers » de la conférence. Les deux chercheurs y introduisent une nouvelle approche pour cartographier des surfaces courbes sur un plan sans cisaillement, permettant des paramétrisations rectangulaires. Cette méthode innovante améliore la qualité du maillage, offre un contrôle utilisateur étendu et surpasse les techniques existantes dans les tâches de simulation, de modélisation et de fabrication numérique.
Dans le domaine de la simulation numérique, le maillage d’un objet est constitué de formes géométriques simples. De manière classique, les maillages triangulaires, ou tétraédriques, sont le plus communément utilisés. Pour certaines applications, les maillages quadrangulaires, ou hexaédriques, constitués de carrés et plus structurés, sont nécessaires, mais ils sont très complexes à obtenir. Ce type de maillage peut être utilisé dans de nombreux domaines, de la simulation numérique à l’architecture, en passant par la retopologie (par exemple dans les films d’animation), la conception textile, ou encore l’optimisation de formes dans des problèmes liés à la science des matériaux.
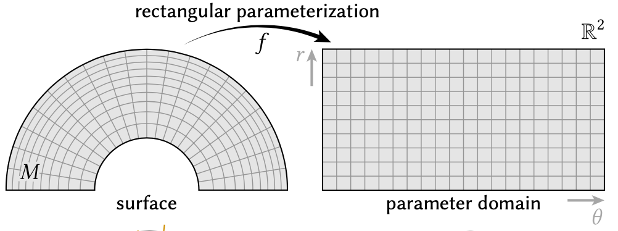Cet article se penche sur un problème classique pour la communauté de la simulation numérique depuis les années 2000, et pour lequel de nombreux algorithmes ont déjà été proposés : le calcul de cartes géographiques pour une surface donnée, c’est-à-dire une correspondance entre chaque point de la surface et un point du plan.
Ce type de carte est utilisé dans des domaines comme la modélisation 3D, la fabrication ou la génération de maillage. « Notre contribution porte sur l’étude de cartes sans cisaillement : un petit carré tracé sur la surface ne peut être déformé qu’en rectangle, et non en parallélogramme quelconque, précise Étienne Corman. Cette propriété est particulièrement intéressante pour générer des maillages quadrangulaires de haute qualité, avec des angles aussi proches que possible de 90°, ce qui améliore la performance des simulations numériques. »
Contrairement aux stratégies passées visant à obtenir l’intégrabilité, les chercheurs obtiennent ainsi des cartes moins déformées et qui préservent mieux les directions. Cette méthode prend en charge les mesures de distorsion définies par l’utilisateur, l’alignement précis des caractéristiques, les singularités coniques prescrites ou automatiques, et le contrôle direct du comportement des limites. Ce résultat dépasse les algorithmes de génération de maillages existants en termes de précision et de qualité des éléments.
Par exemple, ce maillage est particulièrement bien adapté pour la simulation d’écoulement de fluide, comme exposé ci-dessous :
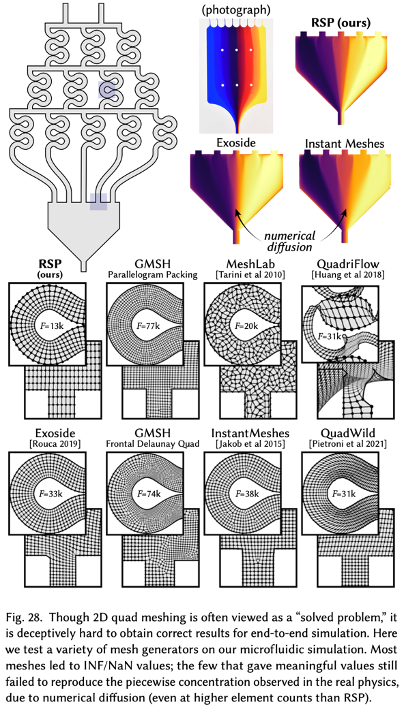
À terme, l’objectif des chercheurs est de pouvoir appliquer ces résultats à la dimension supérieure -la 3D-, un problème extrêmement complexe en raison notamment du temps de calcul, de la discrétisation des équations ou de la topologie de la surface. S’il n’existe actuellement aucune méthode automatique pour la 3D, le résultat présenté dans cet article constitue la première étape de ce défi scientifique !
• Consulter l’article : Rectangular Surface Parameterization.
Etienne Corman, Keenan Crane. Rectangular Surface Parameterization. ACM Transactions on Graphics, 2025, 44 (4), pp.1-21. ⟨10.1145/3731176⟩. ⟨hal-05189504⟩
• Plus d’informations sur le prix sur le site de Siggraph.
• En savoir plus sur Siggraph 2025.
• En savoir plus sur l’équipe Pixel.
• Voir la page personnelle d’Etienne Corman.
